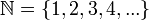LA LEY DE LOS SIGNOS

LA RECTA NUMERICA

LA REGLA DE LOS NUMEROS POSITIVOS EN CUAN MAS GRANDE SEA EL NUMERO MAYOR VALOR TIENE
LA REGLA DE LOS NUMEROS NEGATIVOS MIENTRAS MAS CERCA ESTAN DEL CERO MAS MAYORES SONN

DIVICION DE NUMEROS ENTEROS

LA DIVICION DE NUMEROS ENTEROS ES TAN SENCILLO PUES SU PROPIO NOMBRE LO DICE SE TRATA DE DIVIDIR
EJEMPLO:
(15)·-·(-3) = -5
(4)·-·(2)=  2
(8)·-·(-4)= -2

NUMEROS NATURALES, RACIONALES, IRRACIONALES

Puesto que los números naturales se utilizan para contar objetos, el cero puede considerarse el número que corresponde a la ausencia de los mismos. Dependiendo del autor y la tradición, el conjunto de los números naturales puede presentarse entonces de dos maneras distintas:

Definición sin el cero: Definición con el cero:

LOS NUMEROS ENTEROS SON LOS POSITIVOS & LOS NEGATIVOS
EJEMPLO:



LOS NUMEROS RACIONALES SON LOS NUMEROS FRACCIONARIOS


LOS NUMEROS IRRACIONALES SON:

MATEMATICAS

CUALES SON LOS NUMEROS ENTEROS

Los números enteros son un conjunto de numeros que incluye a los numeros naturales distintos de cero (1, 2, 3, ...), los negativos de los números naturales (..., −3, −2, −1) y al cero, 0. Los enteros negativos, como −1 ó −3 (se leen "menos uno", "menos tres", etc.), son menores que todos los enteros positivos (1, 2, ...) y que el cero. Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo "más" delante de los positivos: +1, +5, etc. Cuando no se le escribe signo al número se asume que es positivo.

El conjunto de todos los números enteros se representa por la letra ℤ = {..., −3, −2, −1, 0, +1, +2, +3, ...}, que proviene del alemán Zahlen ("números", pronunciado [ˈtsaːlən]).